初二（下）首次月考数学试题
1、选择题（本大题12个小题，每小题4分，共48分）在每一个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答卷卡上对应题目的正确答案标号涂黑．
1．（4分）下列计算中，正确的是（）
A．（﹣m2）3＝m6 B．（﹣3mn3）2＝6m2n6
C．﹣m2•žm3＝﹣m6 D．（2m3）2＝4m6
2．（4分）点（﹣3，4）关于y轴对称点是（）
A．（﹣3，4） B．（3，4） C．（3，﹣4） D．（﹣4，3）
3．（4分）如图，在△ABC中，CD是∠ACB的外角平分线，且CD∥AB，若∠ACB＝100°，则∠B的度数为（）
A．35° B．40o C．45o D．50o
4．（4分）函数y
的自变量x的取值范围是（）
A．x≠2 B．x＞2 C．x≥2 D．x＞2且＞x≠3
5．（4分）若一个正多边形的一个内角是140°，则这个正多边形的边数是（）
A．10 B．9 C．8 D．7
6．（4分）估计3
的运算结果在哪两个连续整数之间（）
A．5和6 B．6和7 C．7和8 D．8和9
7．（4分）化简
的结果为（）
A．﹣1 B．5﹣2a C．﹣1﹣2a D．不可以确定
8．（4分）下列图形都是由同样大小的〇按肯定的规律组成，其中第l个图形有3个〇，第2个图形有10个〇，第3个图形有19个〇，算4个图形有30个〇，……根据此规律，第6个图形中共有（）个〇．
A．43 B．55 C．58 D．65
9．（4分）等腰三角形一腰上的高与另一腰的夹角为40°，则它的底角度数是（）
A．65° B．65°或25° C．25° D．50°
10．（4分）如图，在菱形ABCD中，AC与BD相交于点O，AB＝4，BD＝4
，E为AB的中点，点P为线段AC上的动点，则EP+BP的最小值为（）
A．4 B．2
C．2
D．8
11．（4分）重庆因为丘陵、山地的特殊地势，被网友们称为”3D魔幻城市”．在重庆，你有时会看到马路上面是房子、马路下面也是房子；你从底楼出来，看到门口是一条公路，等你坐电梯上到顶楼，发现还是公路．小王家就在这种一栋楼里：他从家底楼出来会看到一条斜坡公路DC，已知∠DCE＝30°，他从楼底B出发，沿着公路到达C处后继续沿着斜坡前进到达D处，共走了27米，然后他又沿着斜坡DA前进到达了顶楼A处，已知DA与水平线夹角为30°，大楼AB高
米，假设BC、CD、AD、AB在同一平面内，则斜坡CD的长度约为（）（已知：
1.73）
A．10.3 B．10.4 C．9 D．9.2
12．（4分）若关于x的方程（a+1）x2+（2a﹣3）x+a﹣2＝0有两个不相等的实根，且关于x的方程
的解为整数，则满足条件的所有整数a的和是（）
A．﹣2 B．﹣1 C．1 D．2
2、填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答卷卡中对应的横线上．
13．（4分）电影《流浪地球》于2019年2月5日在中国大陆上映，该片讲述了在不久的将来太阳马上毀灭，太阳系已经不合适人类存活，而面对绝境，人类将开启“流浪地球”计划，探寻人类的新家园的故事．上映到今天，累计票房收入4640000000元，其中4640000000用科学记数法表示为__________．
14．（4分）计算：（﹣1）2018﹣（2019﹣π）0+（
）﹣2＝__________．
15．（4分）若关于x的一次函数y＝（m+1）x+2m﹣3的图象经过1、3、四象限，则m的取值范围为__________．
16．（4分）已知O（0，0），A（﹣1，5），B（3，﹣3），F点为x轴上的一点，若△AOF的面积等于△AOB面积的一半，则F点的坐标为__________．
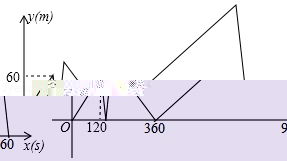
17．（4分）最近，小明和小李报名参加了越野跑比赛，已知两人同时出发，以各自的速度匀速跑步前进，出发一段时间后，小明身体不适，停下来休息了1分钟，再以原速继续跑步前进，当小明到达终点后，立即走路返回去接小李；两人相遇后，小明立即以原来的速度跑步前往终点，1分钟后到达终点．已知两人间的距离y（m）随两人运动时间x（s）变化如图．问：当小明首次到达终点时，小李距终点的距离为__________m．
18．（4分）某公司推出了甲、乙两种新产品饮料，它们都由A、B、C三种溶液组成，只不过甲种饮料每瓶装有200克A溶液，200克B溶液，100克C溶液；乙种饮料每瓶装有100克A溶液，100克B溶液，300克C溶液，甲、乙两种饮料每瓶本钱价均为瓶中A、B、C三种溶液的本钱价之和．已知C种溶液每一百克的本钱价为1元，乙种饮料每瓶价格为10元，利率为
，甲种饮料每瓶的价值率为20%，求这两种饮料的销售利率为24%时，该公司销售甲、乙两种饮料的数目之比是__________．（已知：利率
）
3、解答卷（本大题共8小题，共78分）解答时每小题需要给出必要的演算过程或推理步骤，请将解答过程书写在答卷卡中对应的地方上.
19．（10分）计算：
（1）解不等式组
；
（2）解方程
．
20．（8分）先化简，再求值：
，其实x
2．
21．（8分）如图，在△ABC中，点D，E，F分别是AB，AC，BC的中点，AF⊥BC．求证：四边形ADFE是菱形．
22．（10分）已知关于x的方程kx2﹣（2k+1）x+k+1＝0有两个实数根x1，x2．
（1）求证：x12+x22﹣x1x2
0；
（2）令两根中的较大者为x2，是不是存在实数k，使得
2k＝0成立？若存在，请求出k的值；若没有，请说明理由．
23．（10分）“2018双十一购物狂欢节”，京东商城当天的买卖额约1600亿元．“预计在2020双十一购物狂欢节”京东商城当天的买卖额能达到约1936亿元．
（1）求出2018至2020年京东商城双十一当天的买卖额的年平均增长率；
（2）刘老师在“双十一”到来之前，分别在京东商城的两家店里选了一套标价为1900元的书本和一件标价为990元的羽绒棉服．据悉，双十一当天书本打五五折后再降价
n%．同时，该羽绒棉服店的老板先将羽绒棉服提价
n%，双十一当天再降价
n%，最后刘老师双十一购买两种产品所花费的总金额恰好是1760元．求n的值．
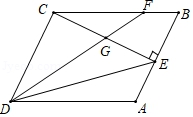
24．（10分）已知，如图在▱ABCD中，点E为AB上一点，连接CE、DE，且CE⊥AB，CE＝AB，点F为BC上一点，连接DF交CE于点G，∠CGD＝∠B；
（1）若CG＝2，AD＝3，求GE的长；
（2）若CF
DE，求证：AD＝CG+BE．
25．（10分）对于给定的函数，自变量取x1，x2时，对应的函数值分别记为y1，y2．自变量取
时．对应的函数值记为，比如一次函数y＝2x+1，自变量取x1，x2时，对应的函数值分别为y1＝2x1+1，y2＝2x2+1，自变量取时，对应的函数值为2•
1，若对于给定的函数，自变量取x1，x2（x1≠x2）时，总有，则称函数为凸凸函数．对于给定的函数总有
，则称函数为凹凹函数．对于给定的函数总有
，则称函数为平平函数．
（1）求证：函数y＝2x是平平函数；
（2）判断函数y＝ax2是凸凸函数，凹凹函数还是平平函数．
26．（12分）如图，直线y＝kx+b与x轴和y轴交于A、B两点，AB＝4
，∠BAO＝45°．
（1）如图1，求直线AB的分析式．
（2）如图1，直线y＝2x﹣2交x轴于点E．且P为该直线在直线AB上方一动点，当△PAB的面积等于10时，将线段PE沿着x轴平移得到线段P1E1，连接OP1．求OP1+P1E1
的最小值．
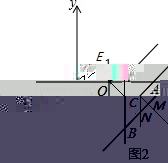
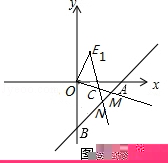
（3）如图2，在（2）问的条件下，若直线y＝2x﹣2与y轴的交点是C，连接CE1，得到△OCE1，将△OCE1绕着原点O逆时针旋转α°（0＜α＜180），旋转过程中直线OC与直线AB交于点M，直线CE1与直线AB交于点N，当△CMN为等腰三角形时，直接写出α的值．
初二（下）月考数学试题
参考答案
1、选择题（本大题12个小题，每小题4分，共48分）在每一个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答卷卡上对应题目的正确答案标号涂黑．
1．D； 2．B； 3．B； 4．B； 5．B； 6．B； 7．D； 8．C； 9．B； 10．C； 11．B； 12．D；
2、填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答卷卡中对应的横线上．
13．____________________； 14．__________； 15．__________
； 16．____________________
__________； 17．__________； 18．；
3、解答卷（本大题共8小题，共78分）解答时每小题需要给出必要的演算过程或推理步骤，请将解答过程书写在答卷卡中对应的地方上.
19．（1）原不等式组的解集是﹣5≤x＜﹣2．
（2）原方程的解为x．
20．﹣2．
21．证明：∵AF⊥BC，点D，E，F分别是AB，AC，BC的中点，
∴AB＝AC，DF
AC＝AE，EFAB＝AD，
∴DF＝AD＝EF＝AE，
∴四边形ADFE是菱形．
22．（1）∵x1+x2
，x1x2
，
∴x12+x22﹣x1x2
＝（x1+x2）2﹣3x1x2
＝（
）2
＝（）2≥0，
即x12+x22﹣x1x20；
（2）存在，理由如下：
∵kx2﹣（2k+1）x+k+1＝0，
∴（x﹣1）（kx﹣k﹣1）＝0，
则x1＝1，x21；
若k＞0，则1
1，
由2k＝0得2k＝0，整理得2k2+k+1＝0，
此方程无解；
若k＜0，则1＞1，
由2k＝0得2k，
解得k
；
综上，存在k，使2k＝0．
23．（1）10%；
（2）m的值为
．
24．（1）GE
；
（2）CF
，
∴∠CDF＝∠CFD＝∠BCE，∠CGD＝∠BCE+∠CFD＝2∠CDF，
∴∠CDF＝30°，
DG＝2CG，BC＝2BE，CG＝BE，
∴AD＝BC＝CG+BE．
即AD＝CG+BE．
25．（1）证明：∵当自变量取x1，x2时，对应的函数值分别为y1＝2x1，y2＝2x2，
当自变量取时，对应的函数值为
2•x1+x2，
∵x1+x2，
∴，
∴函数y＝2x是平平函数；
（2）∵当自变量取x1，x2时，对应的函数值分别为y1＝ax12，y2＝ax22，
∴
（x12+x22），
当自变量取时，对应的函数值为a•
（xx2x1x2），
∴
y（x12+x22）
（xx2x1x2）（x1﹣x2）2，
∵x1≠x2，（x1﹣x2）2＞0，
∴当a＞0时，y（x1﹣x2）2＞0，
∴，则函数y＝ax2为凹凹函数．
当a＜0时，y（x1﹣x2）2＜0，
∴，则函数y＝ax2为凸凸函数．
26．（1）y＝x﹣4，
（2）52．
（3）由题意得：C（0，﹣2），∴OC＝OE1，∠COE1＝90°，
△CMN为等腰三角形，分四种状况：
①∠CNM＝∠NCM＝45°（如图2），旋转角α＝45°；
②∠CNM＝∠CMN＝67.5°（如图3），旋转角α＝67.5°；
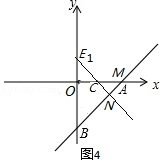
③∠CMN＝∠NCM＝45°（如图4），旋转角α＝90°；
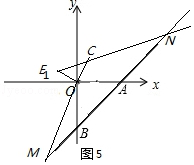
④∠CMN＝∠NCM＝22.5°（如图5），旋转角α＝157.5°
综上所述，旋转角α＝45°，67.5°，90°，157.5°时，△CMN是等腰三角形．
